To calculate the percentile from z score, we look at the value directly from the standard normal table and multiply the value by 100. For example, consider a z score of -1.67. We get the value directly from the table as follows;
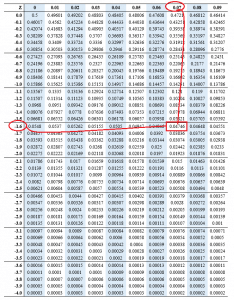
The percentile value coinciding with the z score of -0.67 is 0.04746. Thus, the percentile will be given by;
=0.04746 * 100
=4.746 percentile
How does z score relate to percentile?
Percentiles are similar to quartiles in that they partition the data set into 100 equal parts rather than four equal parts.
Percentiles are useful for determining an individual’s relative standing in a population; they are primarily the rank position of an individual. Similarly, Z-scores assess how exceptional an individual is in comparison to the mean of a population, with the standard deviation for that population used to define the scale.
Notably, the percentiles use the median as the average or the 50th Percentile, while the z score uses the mean as the average, which can be defined as a z score of 0.
A 95th percentile will represent 1.645 z-score of the data.
A z-score of 0 equals a percentile of precisely 0.50.
As a result, a z-score higher than 0 corresponds to a percentile larger than 0.50, while a z-score less than 0 equates to a percentile less than 0.50.
How to convert z score to percentile
To convert z-score to percentile, we look at the value directly from the standard normal table and multiply the value by 100.
Z score to percentile in excel
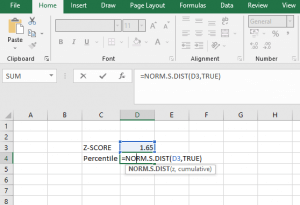
To convert z-score to percentile in excel, we use the built-in Excel function. The z score to percentile formula is =NORM.S.DIST(z, cumulative);
Where:
Z is the z-score of a given data value
Cumulative takes the TRUE value, which returns the cumulative distribution function; The FALSE returns the probability distribution function (PMF). Notably, we use the TRUE value to calculate the percentiles.
For example, convert a z-score of 1.65 to a percentile in excel.
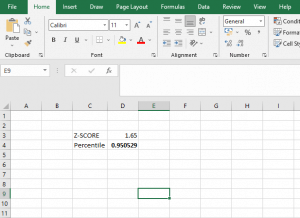
Thus, a z score of 1.65 corresponds to a percentile of 95.0529. This means that a data value with a z score of 1.65 is larger than 95.05% of all other data values available in a given dataset.
Examples
How to find the z score of a percentage
Determine the z score for 80%?
To determine the z score for 80%, we check the value of the percent in the center part of the normal distribution table as depicted in the figure below.
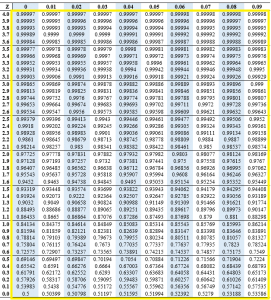
Thus, to find the z score of 80%, we will have;
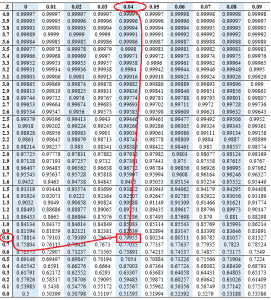
The Z-score for 80% is 0.84
What is the z score for 40%?
We use the same formula by checking the value of 0.4 from the normal distribution table.
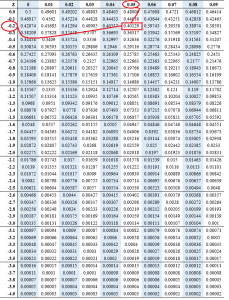
The z score for 40% is -0.25
Find a z-score of 5%
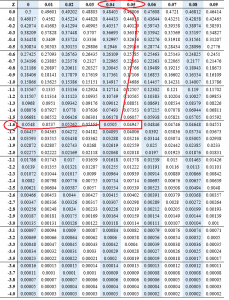
The z-score of 5% will be;
=((-1.64+-1.65)/2)
=(-3.29/2)
=-1.645
What is the z value for 95%?
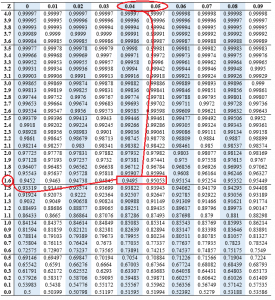
The z-score of 95% will be;
=((1.64+1.65)/2)
=(3.29/2)
=1.645
The z score of 95% is 1.645
What is the z-score of 10 percent?
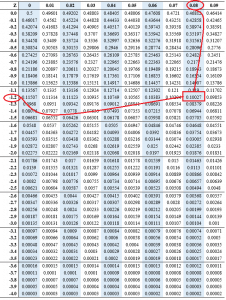
The z score of 10 percent is -1.28
What is the z score for 90%?
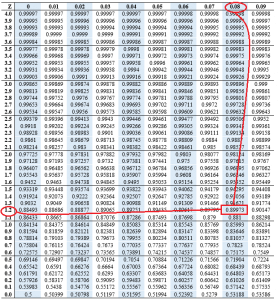
The z score of 90 percent is 1.28
