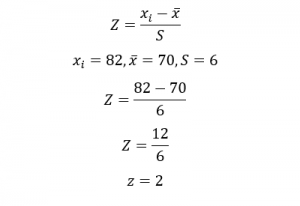How to Calculate z score
The easiest way to find the Z score is by using the formula.
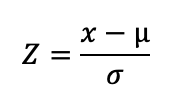
Consider an example given x (the data point) as 20 and the mean to be 40, and the standard deviation as 10. To calculate z-score, we get;
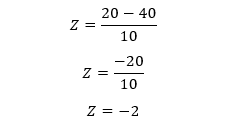
Examples of calculating z score
What is the z-score of -1.25?
The z score of -1.25 is 0.10565. We can obtain the value from the z score table as follows.
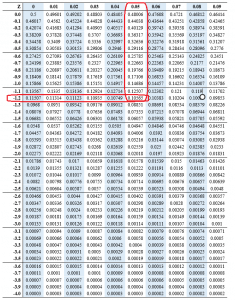
What is the z-score of – 1.0
The z score of -1.0 is 0.15866. We can obtain the value from the z score table as follows.
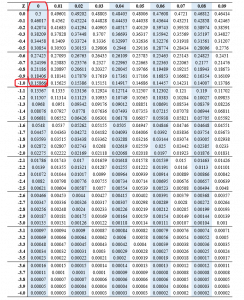
What is the z score of 0.05
The z score of 0.05 is 0.51994. We can obtain the value from the z score table as follows.
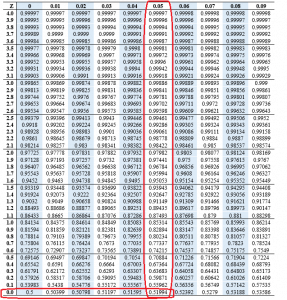
What is the z-score of 0.025
The z score of 0.025 can be checked as the z score of 0.02 and 0.03 and getting the average.
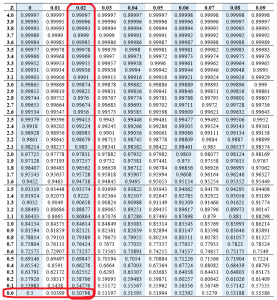
The z score of 0.02
The z score of 0.03
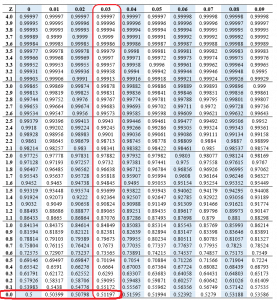
The Z-score of 0.025 = (0.50798+ 0.51197)/2
=0.509975
What is x in z score formula
x in z score formula represents the raw score in the given data. For example, if a student has a test score of 100, and the mean (µ) 0f 125 and a standard deviation (?) of 25. In the formula for calculating the z score, the raw score (x) will be 100 scores.
How to determine z score without x (raw score)
This entails solving for x, given the mean, standard deviation, and z score values. In this case, we shall utilize the z score formula to compute the value of x.
For example, The weekly payments of employees are normally distributed, with a mean of $50 and a standard deviation of $10. Find the x value that corresponds to the z score of 1.
We commence by noting down the formula that we apply;
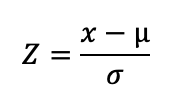
From this z score formula, we can derive the formula for calculating the value of x algebraically;

The value that corresponds to the z-score of 1 is $ 60
The $60 score is statistically correct since it is tentatively 10 points above the mean value ($50).
How to find z-score with mean and standard deviation
In finding the z score with the mean and the standard deviation, we use the z score formula. Consider an example given x (the data point) as 40 and the mean to be 20, and the standard deviation as 10. To calculate z-score, we get;
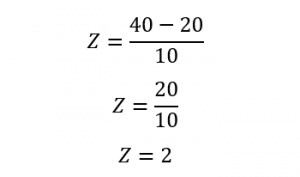
Thus, the z score is 2.
How to find standard deviation given z score
To find the standard deviation given the z score, we use the formula;
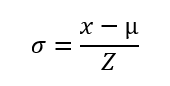
For example, Liam scored 90 on a test and the mean (µ) of 96. The z score value of the test score is -3. Calculate the standard deviation.
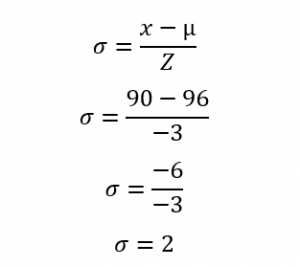
The standard deviation is 2. This means that the test score is two deviations above the mean.
How to find mean given z score and standard deviation
To find the mean given z-score, standard deviation, and the raw value (x), we use the formula;
We commence by noting down the z score formula;
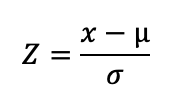
From this z score formula, we can derive the formula for calculating the value of µ algebraically;
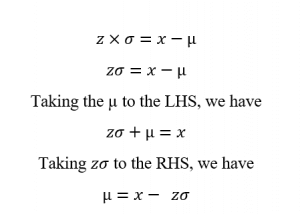
To find the mean given z score, standard deviation, and the raw score, we use the formula;
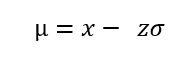
For example, considering the above example of Liam’s scores, he scored 90 on a test, The z score value of the test score is -3, and the standard deviation is 2. Find the mean of the test.
We use the formula;
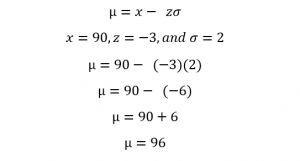
How to find z score of a sample population
To find z score of a sample population is;
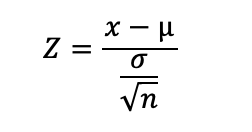
X is the observed mean value
µ is the mean of the sample population
? is the standard deviation of the sample population
n is the number of occurrences or the sample population
For example, a sample of 25 students was put under survey. The population mean of their height is 172cm, and the population standard deviation is 20cm. What is the z score of the sample population for a student of an observed height of 176 cm?
X is the observed value= 176cm
µ is the mean of the sample population= 172cm
? is the standard deviation of the sample population= 20cm
n is the number of occurrences or the sample population= 25 students
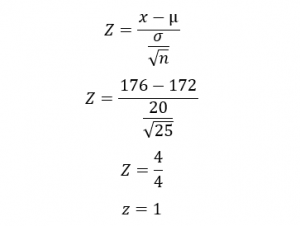
This depicts that height is one standard deviation from the mean.
Sample mean z score formula
The sample mean z score formula is the same formula as the z score formula except that the µ (population mean) changes to (sample mean) and ? (the population standard deviation) changes to S (the sample standard deviation). However, solving the z score values follows the exact steps. Thus, the formula of the sample mean z score formula is;
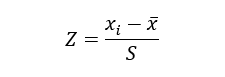
For example, on the statistics exam, the sample mean score was 70 and a sample standard deviation of 6. If a student’s actual score of 82, what is her z-score?
We use the formula