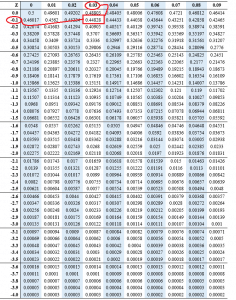
To find z score for percentile, we check the percentile value in the center part of the normal distribution table. For example, find the z score of the 45th percentile.
The Z score for the 45th percentile is -0.13
Example two, find the z score of the 33rd percentile.
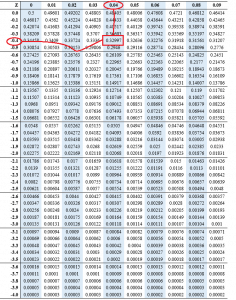
The Z score for the 33rd percentile is -0.44
Percentile to z score formula
The formula of percentile to z score formula assumes that the underlying distribution is normal. The formula to calculate percentile to z score is given by;
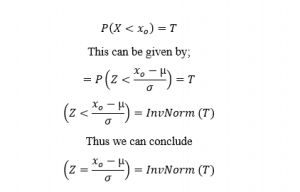
Where T is the percentile
Notably, we can find the value of the z score of a percentile in excel using the excel function =Norm.Inv (T,0,1)
Where T is the percentile
0 is the standard mean
1 is the standard deviation
For example, consider the 40th Percentile, and find the z score in excel.
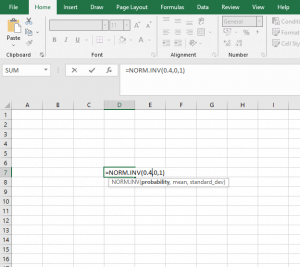
Thus, the value will be;
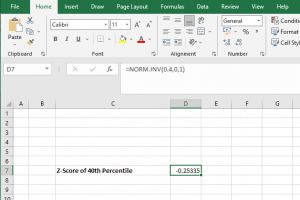
The Z-score for the 40th percentile is -0.25335
Examples to find z score for percentile
What z score represents the 95th percentile
The z-score that represents the 95th Percentile is 1.645
What z score represents the 90th percentile
The z-score that represents the 90th Percentile is 1.282
What z score represents the 80th percentile
The z-score that represents the 80th Percentile is 0.842
What z score represents the 75th percentile
The z-score that represents the 75th Percentile is 0.674
What z score represents the 85th percentile
The z-score that represents the 85th Percentile is 1.036
What z score represents the 20th percentile/2nd decile
The z-score that represents the 20th Percentile is -0.842
Z score percentile table/chart
| Percentile | Z-Score | Percentile | Z score |
| 1 | -2.326 | 51 | 0.025 |
| 2 | -2.054 | 52 | 0.05 |
| 3 | -1.881 | 53 | 0.075 |
| 4 | -1.751 | 54 | 0.1 |
| 5 | -1.645 | 55 | 0.126 |
| 6 | -1.555 | 56 | 0.151 |
| 7 | -1.476 | 57 | 0.176 |
| 8 | -1.405 | 58 | 0.202 |
| 9 | -1.341 | 59 | 0.228 |
| 10 | -1.282 | 60 | 0.253 |
| 11 | -1.227 | 61 | 0.279 |
| 12 | -1.175 | 62 | 0.305 |
| 13 | -1.126 | 63 | 0.332 |
| 14 | -1.08 | 64 | 0.358 |
| 15 | -1.036 | 65 | 0.385 |
| 16 | -0.994 | 66 | 0.412 |
| 17 | -0.954 | 67 | 0.44 |
| 18 | -0.915 | 68 | 0.468 |
| 19 | -0.878 | 69 | 0.496 |
| 20 | -0.842 | 70 | 0.524 |
| 21 | -0.806 | 71 | 0.553 |
| 22 | -0.772 | 72 | 0.583 |
| 23 | -0.739 | 73 | 0.613 |
| 24 | -0.706 | 74 | 0.643 |
| 25 | -0.674 | 75 | 0.674 |
| 26 | -0.643 | 76 | 0.706 |
| 27 | -0.613 | 77 | 0.739 |
| 28 | -0.583 | 78 | 0.772 |
| 29 | -0.553 | 79 | 0.806 |
| 30 | -0.524 | 80 | 0.842 |
| 31 | -0.496 | 81 | 0.878 |
| 32 | -0.468 | 82 | 0.915 |
| 33 | -0.44 | 83 | 0.954 |
| 34 | -0.412 | 84 | 0.994 |
| 35 | -0.385 | 85 | 1.036 |
| 36 | -0.358 | 86 | 1.08 |
| 37 | -0.332 | 87 | 1.126 |
| 38 | -0.305 | 88 | 1.175 |
| 39 | -0.279 | 89 | 1.227 |
| 40 | -0.253 | 90 | 1.282 |
| 41 | -0.228 | 91 | 1.341 |
| 42 | -0.202 | 92 | 1.405 |
| 43 | -0.176 | 93 | 1.476 |
| 44 | -0.151 | 94 | 1.555 |
| 45 | -0.126 | 95 | 1.645 |
| 46 | -0.1 | 96 | 1.751 |
| 47 | -0.075 | 97 | 1.881 |
| 48 | -0.05 | 98 | 2.054 |
| 49 | -0.025 | 99 | 2.326 |
| 50 | 0 |
What is a percentage rank?
Percentile rank (PR) of a given score in statistics refers to the proportion of scores lower than a given score in a frequency distribution.
To make the meaning of test results more understandable, percentile ranks are frequently used.
According to the test theory, the percentile rank of a raw score is understood to be the proportion of test-takers in the norm group who received a score lower than the score of interest.
Statistics professionals frequently use percentile rank to determine how an individual assessment score or outcome relates to others in a set.
Additionally, knowing the percentile rank can help one gain perspective on how well they did on a particular test.