To convert the z score to percentile in r, we use the built-in formula: Pnorm (z-score)
Example 1: Convert 1.28 z score to percentile in R
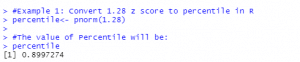
The Z score of 1.28 corresponds to a percentile of 0.8997274. We interpret this to mean that a z-score of 1.28 is larger than 89.97% of the other values in the given dataset.
Example 2: Convert 1.0 z score to percentile in R
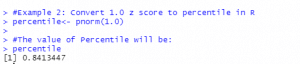
The Z score of 1.0 corresponds to a percentile of 0.8413447. We interpret this to mean that a z-score of 1.0 is larger than 84.13% of the other values in the given dataset.
Example 3: Convert 2.25 z score to percentile in R
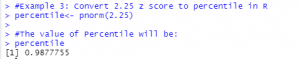
The Z score of 2.25 corresponds to a percentile of 0.9877755. We interpret this to mean that a z-score of 2.25 is larger than 98.78% of the other values in the given dataset.
Percentile to Z score in R
To convert percentile to Z score, we use the built-in formula: qnorm (percentile)
Example 1: Convert a percentile of 0.10 to a Z-score in R
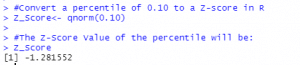
A percentile of 0.10 corresponds to a Z-Score of -1.281552. This means that a dataset’s data value at the 10th percentile has a Z-Score of -1.281552, which depicts it as approximately 1.2 standard deviations below the mean.
Example 2: Convert a percentile of 0.50 to a Z-score in R
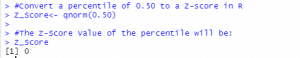
A percentile of 0.50 corresponds to a Z-Score of 0. This means that the data value at the 50th percentile in a dataset has a Z-Score of 0, which depicts it is at the mean.
Example 3: Convert a percentile of 0.76 to a Z-score in R
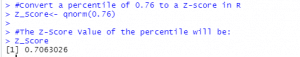
A percentile of 0.76 corresponds to a Z-Score of 0.7063026. This means that a dataset’s data value at the 76th percentile has a Z-Score of 0.7063026, which depicts it as approximately 0.7 standard deviations above the mean.
