Definition of z score
A Z-score is a numerical measurement that defines the relationship between a value and the mean of a set of values.
The z-score will tell us how far the score deviates from the mean in standard deviations and in which direction it deviates.
Raw scores are converted into standard deviation units above or below the mean using Z-scores. The standard normal distribution is used as a reference in this transformation.
What does a z score measure?
Z-score measures the number of standard deviations from the mean. The z-score can be defined as the numerical measurement of the relationship between a group of values and the mean.
Notably, if the value of the z-score is 0, it means that the data point score corresponds to the mean.
Alternative names of z score
The z-score is sometimes known as the bell curve, standard normal curve, standardized score, z score critical value, normal score, Z-value, Standard score, standardized variable, or the Altman z score.
What is the formula of a z score?
The basic Z score formula for a sample is:
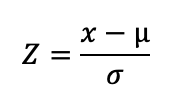
Z is the standard score
X is the observed value
μ is the mean of the sample
σ is the standard deviation of the sample
Different Z-Score formulas and equations for Multiple Samples
The Z-score formula for multiple samples describes the standard deviation of the sample means. The z score tells us the number of standard errors there are between the sample mean and the population means.
The Z-Score formula for Multiple Samples is;
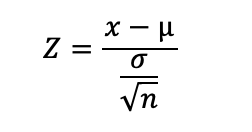
How to find the mean given z score and Standard deviation
Example 1:
For example, if a student scores a 150 on a test where the mean of the test μ is 100 and the
standard deviation (σ) is 20.
Calculating the z-score will be;
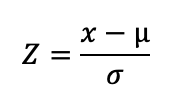
X is the observed value = 150
μ is the mean of the sample = 100
σ is the standard deviation of the sample = 20
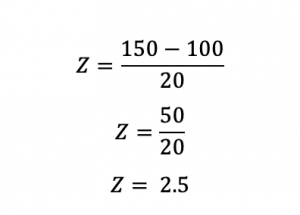
Example 2:
For example, the mean weight of women is 170 with a standard deviation of 7. Assuming the weights are normally distributed, what is the probability of finding a random sample of 60 women with a mean weight of 180?
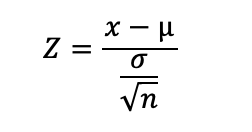
X is the observed mean value = 180
μ is the mean of the samples = 170
σ is the standard deviation of the samples = 7
n is the number of occurrences =60
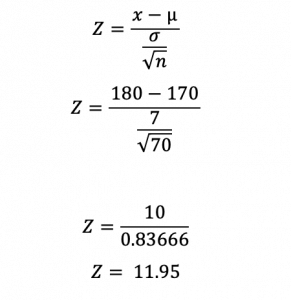
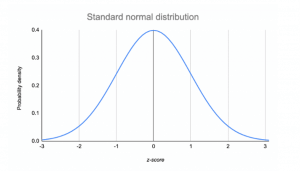
Range of Z score
The z score ranges from -3 standard deviations on the left of the normal distribution curve up to +3 standard deviations, which is far right of the normal distribution curve.
Thus a data point can be considered unusual if its z-score is above three or below -3.
Uses of a z-score
The z score is a crucial statistic. It is used to:
- Gives us an idea of how far from the mean a data point is.
- Enable us to compare scores that are from various normal distributions
- It facilitates calculating the probability of a score in the normal distribution.
Z score in Statistics
A Z-score is a numerical measurement that shows the relation between a value and the mean of a set of values. The standard deviations from the mean are used to calculate the Z-score.
A Z-score of 0 means that the data point’s score is the same as the mean score. The z score tells us the number of standard deviations away from the mean in statistics.
Notably, a positive z-score depicts the raw score is higher than the mean average. For example, if a z-score equals +2, it is two standard deviations above the mean.
After calculating the z score value, we can look for the probability using the z score table.
Z-Score in Finance
Z-scores are indicators of an observation’s variance used by traders to determine market volatility in finance. A Z-score can tell a trader whether a number is normal or uncommon for a certain data collection.
A Z-score below 1.5 indicates that a company is on the verge of bankruptcy, whereas a score closer to 3 indicates that the organization is in good financial shape.
Moreover, the Altman Z score value in finance is crucial since it depicts whether a company is headed to bankruptcy or profitability.
This value considers solvency, account profitability, leverage, liquidity, and activity ratios.
Measurement units of Z score
There are no units in a z-score. The z score depicts the number of standard deviations from the mean. The region beneath the probability curve within two standard deviations of the mean is represented by z= ±2.
Properties of Z score
- The standard deviation of the z-scores is always 1.
- The mean of the z-score is always 0.
- The sum of the squared z-scores is always equal to the number of z-score values.
- The graph of the z-score distribution always has the same shape as the original distribution of the sample values.
Factors determining the size of a z score
The size of the z-scores depends on three factors: the size of the standard deviation, the raw scores deviation, and the mean of the data points or values.
The mean and the standard deviation are inversely proportional to the z score, while the raw score is directly proportional to the z score.
This means that when the raw score increases, the value of the z score increases. Conversely, when the mean and the standard deviation values increase, the value of the z score decreases.
